1) Prime & Composite Knots: The Connected Sum
Similarly to how we think of counting numbers as being prime or composite, we use the same terms to refer to types of knots.
A composite knot is a knot which can be formed by the composition (joining) of two or more nontrivial knots.
The square knot at the right is an example of a composite knot. It can be formed by cutting one side of two trefoil knots and joining the loose ends of each knot to the other. This forms what is known as a connected sum.
|
The square knot at the right is an example of a composite knot. It can be formed by cutting one side of two trefoil knots and joining the loose ends of each knot to the other. This forms what is known as a connected sum. |
When we join knots to form a composite knot, the process can be referred to as a connected sum – we have combined two or more knots by connecting them on a side. The knots that make up a composite knot are called factor knots.
If a knot is not composite, meaning it cannot be expressed as the connected sum of other knots, we call it a prime knot. The trefoil knot is a prime knot.
2) Stick Knots
Scientists and mathematicians alike are interested by this Knot Theory topic. A stick knot is just what it sounds like – a knot formed out of straight sticks instead of flexible rope.
The reason scientists are intrigued by this kind of knot is that at the microscopic level, molecules are more similar to rigid sticks than flexible rope. For example, the long, curly DNA strand is actually made up of small rigid “sticks” of sugar, phosphorus, nucleotide proteins and hydrogen bonds. (Jump to the DNA & KT Today page if you want to read more on this topic.) Similarly, chemists working on creating synthetic materials from molecular structures of specific shapes are interested in rigid formations of knots.
Forming knots from sticks brings us to another interesting invariant of knots – the stick number. The stick number of any knot is the least number of straight sticks necessary to form the knot.
The trefoil knot (drawn as a stick knot to the right) has a stick number of 6, meaning we need at least 6 sticks to form the trefoil. (In fact, the trefoil knot is the only knot with a stick number of 6.)
An interesting fact for you to study is that no nontrivial knot can be formed by less than 6 sticks. In other words, if you join 5 sticks at the ends, you can never form a knot other than the unknot, no matter how hard you try.
Unanswered Questions:
There are still many unanswered questions concerning stick numbers. In fact, we only know the stick number for a surprisingly small handful of knots. For example, we know that at least 35 knots can be formed from 10 or fewer sticks, but we do not yet know how many more might be in this group.
Also, it is not known whether the stick number changes for some knots when we add the requirement that all sticks be the same length. (The trefoil’s stick number remains 6 with all sticks the same length, but we do not know if this is so for other knots.)
Unanswered questions like these make Knot Theory an interesting field for mathematicians young and old – there is still much to be discovered about knots, and many opportunities to become a famous knot theorist by being the first to explain or describe a phenomenon or property.
3) Wild Knots
In number 1 above, we saw what happens when we join two knots in a connected sum. We get another knot. In number 2 above, we saw how knots can be represented with straight lines, or sticks. Both of these concrete concepts can help us begin to grasp a more abstract concept.
We mentioned at the beginning of the Intro to Knot Theory that a knot is a simple closed curve in 3-dimensional space, and you can see many examples of these knots throughout the site. In addition, all of the knots you will find in this site are what are called tame knots. A tame knot is a knot that can be represented as a polygonal path in 3-dimensional space.
In other words, a tame knot is one that you can form with a finite number of sticks like the trefoil knot in number 2 above. Tame knots are the ones we can build and study out of a set length of rope or other material.
An interesting area of theoretical knots in math opens up when we consider knots that are not tame. What might happen if we started connecting knots infinitely? What if we added two trefoil knots together in a connected sum, then joined one trefoil to each of those, then one to each of those, and so on. When we start crossing over to infinity, we enter the realm of wild knots. A wild knot is any knot that is not tame – that is, that cannot be represented as a polygonal path in 3-dimensional space.
One interesting wild knot to consider begins with the unknot. What if we make loops in the unknot that cross one another? With a tame unknot, we can untangle the loops using the Reidemeister moves. What if we take an infinitely long unknot and continue to make crossing loops an infinite number of times. Will we eventually have something other than the unknot? As the number of loops goes to infinity, will we be able to untangle them all using the Reidemeister moves?
Very little is known about wild knots so far, making this an interesting topic for aspiring knot theorists to study. What might some of the properties of wild knots be? Are there any real-world applications of wild knots? These questions and many more remain to be answered.
4) Coloring Knots and Links
 Mathematicians seem to have a continuing interest in coloring – from graphs to maps to… yes, even knots and links.
Mathematicians seem to have a continuing interest in coloring – from graphs to maps to… yes, even knots and links.
What interests us in Knot Theory in particular is the idea of tri-colorability. A knot or link is called tri-colorable if it is possible to do the following:
Color every strand in the diagram of the knot or link,
Use a total of three colors (hence tri-colorable),
At each crossing, either make all the strands one color or make each strand a different color.
The trefoil knot is tri-colorable, as shown above. It turns out that every trefoil knot in every projection is tri-colorable. In fact, tri-colorability is another knot invariant – it does not change no matter how much we deform the knot.
Since tri-colorability is an invariant, if we can tri-color one projection of a knot, we can tri-color every projection. And, if we cannot tri-color a projection of a knot, then no projection of that knot can be tri-colored.
The unknot cannot be tri-colored (try this to verify). Since the trefoil is tri-colorable, and the unknot is not tri-colorable, we therefore conclude that the trefoil knot is not the unknot.
This last sentence is an important statement. All along, we have been claiming that various knots were different. Now, for the first time we have proven that the unknot and the trefoil knot are different. In a sense, we have proven that knots exist. This is an important point in Knot Theory, and it all came about from playing with colors. Isn’t mathematics beautiful?
5) Some References for Further Study
The following references are those I have used in research for building this site. Each one of these print resources is a valuable reference for studying Knot Theory in greater depth. For online resources on Knot Theory, check out the “Links” to Other Great Knot Sites section of the Fun page.
Colin C. Adams, The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, W.H. Freeman and Company, Oxford, 1994.
Colin Adams, Eric Furstenberg, Jie Li, and Jodi Schneider, “Exploring Knots”, The Mathematics Teacher, National Council of Teachers of Mathematics, November 1997.
David W. Farmer, Knots and Surfaces: A Guide to Discovering Mathematics, American Mathematical Society, 1996.

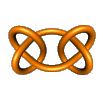
 +
+
